What Is Special About the Baby Maker Bl2
The Birthday Problem🎈
Today's problem goes out to a special new member of the family. Welcome to the globe my niece, Edison Grace Berry! My blood brother's beautiful baby daughter was built-in on his 36th birthday this past Sabbatum and of course this coincidence made me think of the Birthday Problem .
So hither it is: a special math problem for a special picayune girl. Anytime you'll know all the math to understand this post (trust me, I'll make sure of it!).
→ For more math tutorials, check out Math Hacks on YouTube! ←
The Birthday Problem in Real Life
The first fourth dimension I heard this problem, I was sitting in a 300 level Mathematical Statistics course in a small university in the pacific northwest. It was a class of well-nigh 30 students and the professor bet that at to the lowest degree two of us shared the same birthday.
He and then proceeded to take everyone state their birthday. When information technology came to my turn I stated my birthdate equally "2 cubed, three cubed," which fabricated the class express mirth as our cerebral professor took awhile to decipher the engagement.
Anyhow like he predicted earlier he got to the last student a pair of matching birthdays had been found.
So how lucky was information technology that he institute a matching pair?
Warm-Upwardly
Assumption: for the sake of simplicity nosotros'll ignore the possibility of being built-in on Feb. 29th.
Allow's begin with a simple example to warm up our brains:
What is the probability that two people share the same altogether?
Person A can be born on any day of the year since they're the first person we're asking. The probability of being built-in any twenty-four hours of the year is one or more specifically: 365/365.
Since Person B must be built-in on the same 24-hour interval every bit Person A their probability is 1/365.
Nosotros desire both of these events to happen so multiply the probabilities:
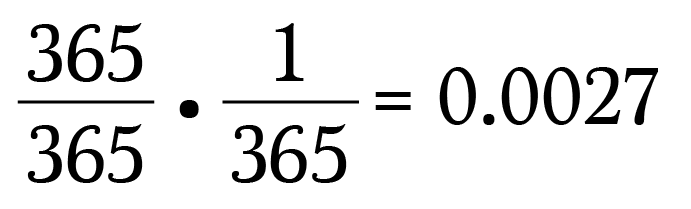
Then you have a 0.27% risk of walking up to a stranger and discovering that their birthday is the same mean solar day every bit yours. That'southward pretty slim.
Merely what about a larger grouping?
What's the chance that at to the lowest degree two out of four people share the aforementioned altogether?
Well to solve this problem nosotros'd take to calculate all of the following:
- Probability A and B share the same birthday
- Probability A and C share the aforementioned altogether
- Probability A and D share the same altogether
- Probability B and C share the same birthday
- Probability B and D share the aforementioned birthday
- Probability C and D share the aforementioned birthday
- Probability A, B and C share the same birthday
- Probability B, C and D share the same birthday
- Probability A, C and D share the same altogether
- Probability A, B and D share the same birthday
- Probability A, B, C and D all share the same altogether
Yuck, that'southward a lot of calculations! Imagine how many probabilities we'd take to calculate for a classroom of 30 students!
In that location'due south gotta exist a better way…
A Better Way: the Trick of the Complement
The simplest way of getting around computing a bajillion probabilities is to expect at the trouble from a different bending:
What's the probability that no one shares the same birthday?
This alternate exercise is helpful because it is the complete opposite of our original problem (i.e. the complement). In probability, we know that the total of all the possible outcomes (i.eastward. the sample space) is always equal to ane, or 100% take chances.
Since the probability of at to the lowest degree 2 people having the aforementioned birthday and the probability of no ane having the same birthday cover all possible scenarios, we know that the sum of their probabilities is ane.
Or equivalently:
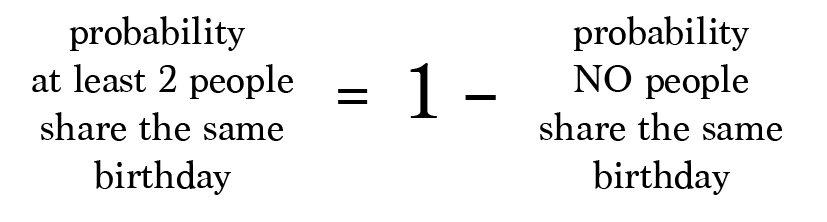
Yay! That'll be much easier to calculate.
The Calculation
Crawly! Nosotros're finally prepare to find out how safe a bet the professor made.
Let'due south piece of work out the probability that no one shares the same birthday out of a room of 30 people.
Permit's have this step by step:
- The first student can be born on whatsoever 24-hour interval, and so we'll give him a probability of 365/365.
- The next student is now limited to 364 possible days, so the second student's probability is 364/365.
- The 3rd educatee may exist built-in on any of the remaining 363 days, so 363/365.
This pattern continues so that our last student has a probability of 336/365 (365 – 29 days since the students before her used upwards 29 potential days).
Once again multiply all 30 probabilities together:
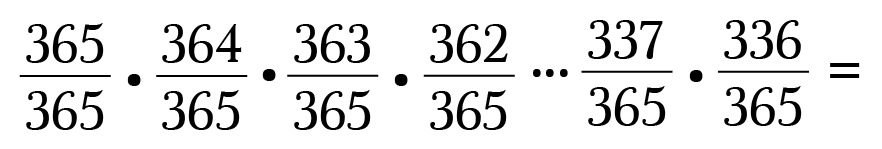
Hold up! That's a picayune messy. Allow's clean this upwards.
Since the denominator is thirty 365'southward multiplied together, we could rewrite it as:

Let'southward utilize factorials (symbolically: !) to further clean this calculation up.
(Recollect factorials are handy for multiplying together descending positive integers. For example five! equals 5•four•3•2•1 = 120.)
Using factorials, 365! would equal the product of all descending integers from 365 down to 1. We merely want the product of the integers from 365 to 336, and so nosotros'll divide out the extraneous numbers by dividing 365! past 335!.

Note: if this confuses you lot effort a smaller value like 5!/3! = 5•iv•three•2•1 / three•2•1. Notice how the 3•2•1 are in both the numerator and denominator. They 'abolish out' making 5!/three! = v•4.
Putting it all together we now have an expression that tin be easily entered on a scientific calculator:

This computes to 0.294 or 29.4% chance no one in the class has the same birthday. Of form, we want the complement so we'll subtract it from i to notice the probability that at to the lowest degree 2 people in a group of 30 share the same mean solar day of birth.

Turns out it was a pretty prophylactic bet for our professor! He had a nearly 71% run a risk that 2 or more of us would share a altogether.
A Fifty-Fifty Adventure
Many people are surprised to discover that if you repeat this adding with a group of 23 people you lot'll still have a 50% hazard that at least ii people were born on the aforementioned day.
That's a relatively pocket-size group of people because that at that place are 365 possible birthdays! Significant that in any grouping of more than 23 people information technology is likely that at to the lowest degree ii people share the same solar day of nascency.
What a crazy little factoid!
❤ STAY Connected ❤
Stay upward-to-date with everything Math Hacks is up to!
Instagram | Facebook | Twitter
Related Reading
Source: https://medium.com/i-math/the-birthday-problem-307f31a9ac6f
0 Response to "What Is Special About the Baby Maker Bl2"
Post a Comment